Александра Лебо: За хороший вирус готова поставить пятерку
Физико-математические модели.
Введение в Математическое моделирование и роль вычислительного эксперимента.
Лебо А.И., к ф-м н
Важную роль в изучении закономерностей объективного мира играет математическое моделирование. Наряду с теорией и практикой математическое моделирование является одним из основных методов познания.
Суть методологии математического моделирования, согласно высказыванию академика А.А. Самарского, состоит в замене исходного объекта исследования его «образом» — математической моделью, — и дальнейшим изучением этой модели с помощью реализуемых на компьютерах вычислительных алгоритмов.
Этот метод сочетает в себе многие достоинства двух других, а именно: а) работа не с самим объектом, а с его моделью, позволяет оперативно и безболезненно исследовать его свойства и поведение в любых мыслимых ситуациях (что присуще теоретическому методу); б) мощные ЭВМ позволяют проводить вычислительные эксперименты, то есть подробно, разносторонне и глубоко изучать объекты (что доступно лишь современному натурному эксперименту). Основным инструментом познания в математическом моделировании является «вычислительный эксперимент» (как теоремы и доказательства в теории, наблюдения и измерения в практике). При этом, «практика» остается «критерием истинности», то есть «завершающим звеном в цепи познания».
Проведение натурных экспериментов является основным инструментом исследования практики, как метода познания. Однако современные эксперименты требуют, как правило, существенных материальных затрат, а новизна и ценность работы в значительной степени зависят от наличия дорогостоящего оборудования, подготовки обслуживающего персонала, наличия необходимых материалов.
Важным достоинством вычислительного эксперимента является его дешевизна и относительная простота. К тому же, если речь идет о ядерных испытаниях, крупных технологических или социально-экономических проектах, то полномасштабное экспериментальное исследование оказывается невозможными.
В последние десятилетия происходит бурное развитие информационных технологий – переработки, передачи и хранения больших потоков информации. На государственном, а в ряде случаев и на международном уровнях, создаются большие корпоративные информационные системы органов управления и обработки информации. Аппаратно-программные решения позволяют не только обрабатывать и представлять в доступной для человека форме результаты, но и создают обратную связь, то есть позволяют по-новому организовать управление большими технологическими, экономическими и социальными системами.
Нужны надежные методы анализа и переработки потоков информации, возможность прогнозирования глобальных явлений на основе полученной информации. Математическое моделирование «может и должно быть интеллектуальным ядром информационных технологий».
Элементами математического моделирования пользовались математики еще с древних времен. Само слово «алгоритм» происходит от имени средневекового арабского ученого Аль-Хорезми. Однако формирование математического моделирования, как самостоятельной методологии произошло в конце 40-х – начало 50-х годов ХХ века и было обусловлено потребностью решения сложных научно-технологических задач по созданию ядерного оружия и средств его доставки до цели, а также задаче запуска и возвращения на Землю космонавтов. Создание и развитие электронно-вычислительной техники, в значительной степени, стимулировалось потребностью быстрого решения этих стратегических задач. И надо отметить, что математическое моделирование справилось с этими грандиозными проблемами – ядерные взрывы, запуски спутников на заданные орбиты, а затем полеты и возвращение на Землю космонавтов были сначала промоделированы с помощью ЭВМ, а затем уж реализованы на практике.
Начиная со второй половины 80-х годов произошел качественный скачок в развитии вычислительной техники – появились персональные компьютеры, мощные параллельные супер-ЭВМ и электронные средства хранения информации огромных объемов. Были созданы новые подходы и программные средства обработки большого объема информации и их наглядного графического представления. Это стимулировало развитие информационного общества, причем его существование и устойчивое развитие, в значительной степени, зависит от освоения и эффективного использования информационных ресурсов. Математическое моделирование становится «интеллектуальным ядром» информационных технологий, позволяющим решать сложные естественнонаучные и социально-экономические задачи.
Проведение вычислительного эксперимента требует четкого плана действий. Можно выделить три основные этапа: 1) модель, 2) алгоритм, 3) программа. На Рис. 2.1 показана схема таких исследований:
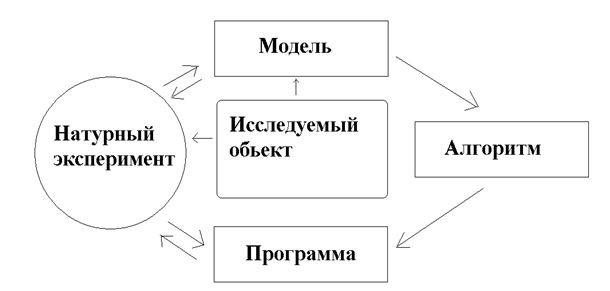
Рис. 2.1. Схема методологии исследования объекта с помощью вычислительных экспериментов
На первом этапе формируется некий теоретический эквивалент исследуемого объекта, на втором этапе происходит выбор и разработка алгоритма для реализации модели на компьютере, на третьем этапе происходит непосредственно написание программы и проведение расчетов. Вычислительный эксперимент, как правило, проводится в тесном взаимодействии с натурным экспериментом на этапах постановки задачи и выполнения вычислений.
Проведение вычислительного эксперимента требует от исполнителей высокой квалификации в различных областях знаний – физике, аналитической и прикладной математике, информатике и т.д. Каждый этап «триады» использует соответствующие технологии и подходы. Можно сформулировать общие принципы, которым должны удовлетворять эти технологии.
На первом этапе важно, чтобы разработанная модель была:
а) актуальной, б) объективной и непротиворечивой, в) существовала возможность проверки ее отдельных положений или частей с помощью натурного эксперимента.
На втором этапе созданные алгоритмы должны удовлетворять принципам: а) адекватности модели, б) экономичности, в) адаптивности.
При написании конкретной программы (третий этап) также должны быть удовлетворены принципы экономичности и адаптивности.
Физико-математические модели описываются, как правило, с помощью систем дифференциальных уравнений в частных производных (ДУЧП). Эффективным методом решения таких уравнений является метод конечных разностей, когда дифференциальное уравнение заменяется его разностным аналогом. В результате, решение исходной системы ДУЧП сводится к решению большого числа алгебраических уравнений, что оказывается под силу современным ЭВМ. Следует отметить, что наряду с разностными методами, возможны и другие подходы к решению ДУЧП.